Doctoral Research

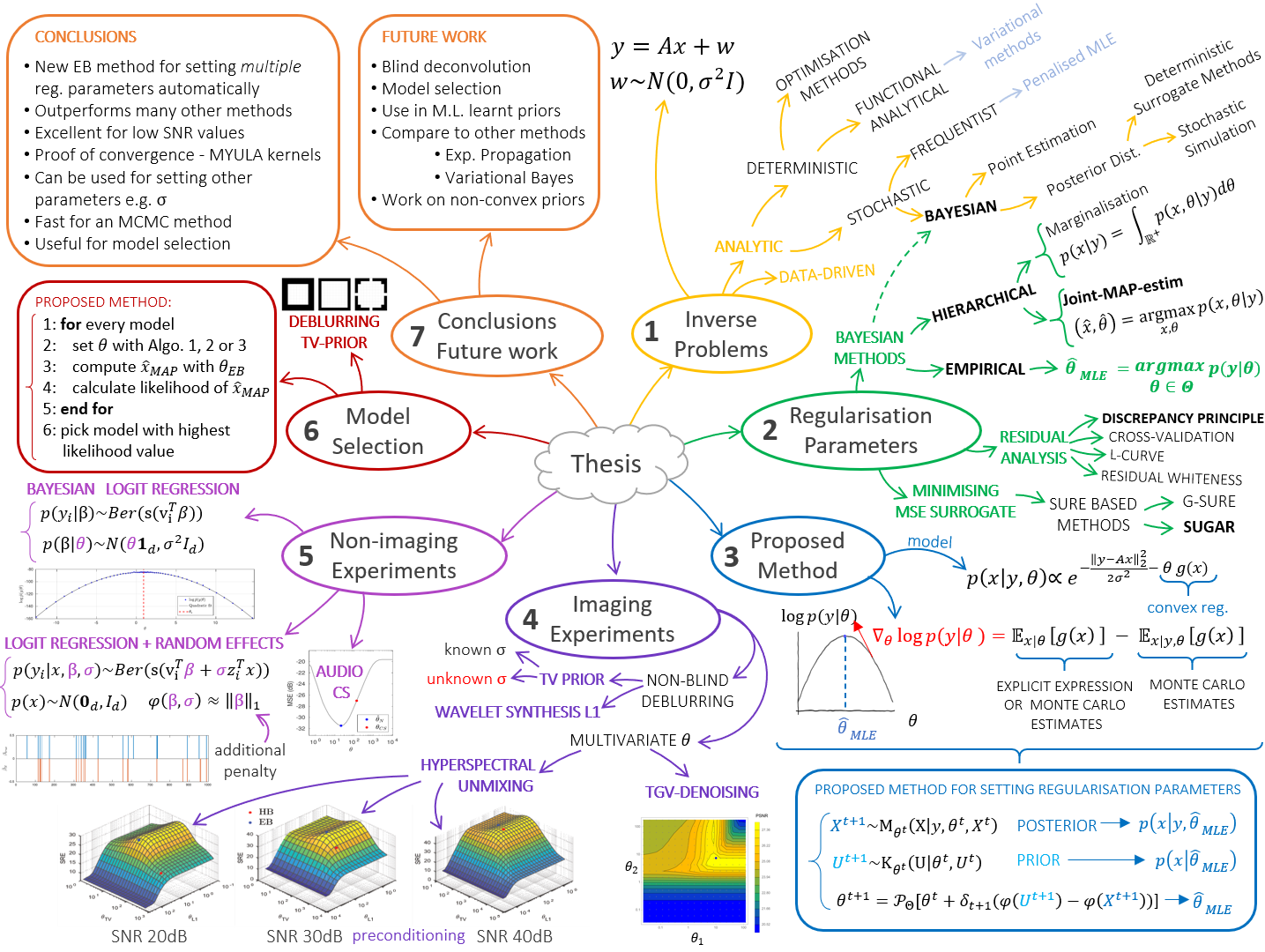
Bayesian computation in imaging inverse problems with partially unknown models

Mathematical imaging is at the core of modern data science, with important applications in medicine, biology, defense, agriculture and environmental sciences. This active research field studies imaging inverse problems involving the estimation of an unobserved true image from measurements that are noisy, incomplete and resolution-limited. My Ph.D. focused on the development of new Bayesian computation methodology for ill-posed high-dimensional inverse problems, with a focus on methods that tightly combine modern high-dimensional stochastic simulation and optimization, and which support advanced Bayesian analyses.

If you are interested in reading more about this you can see my PhD Thesis.

Post-doctoral Research

After my PhD I joined the Offshore Robotics for Certification of Assets (ORCA) Hub project as a Research Associate in eXplainable AI (XAI) and worked in developing transparent machine learning algorithms for NLP and topic modelling.

I worked in the Strategic Futures Laboratory. You can check out our topic map for exploring COVID-19 research.

Publications

• A. F. Vidal, M. Pereyra, A. Durmus and J.F. Giovannelli, “Fast Bayesian model selection in imaging inverse problems using residuals'', To appear in Proc. 2021 IEEE Statistical Signal Processing Workshop (SSP), Jul. 2021.
• A. F. Vidal, V. De Bortoli, M. Pereyra and A. Durmus, “Maximum likelihood estimation of regularisation parameters in high-dimensional inverse problems: an empirical Bayesian approach. Part I: Methodology and Experiments'', SIAM Journal on Imaging Sciences, 13(4), 1945-1989, Nov. 2020.
• V. De Bortoli, D. Alain, M. Pereyra, and A. F. Vidal, “Maximum likelihood estimation of regularisation parameters in high-dimensional inverse problems: an empirical Bayesian approach. Part II: Theoretical Analysis'', SIAM Journal on Imaging Sciences, 13(4), 1990-2028, Nov. 2020.
• De Bortoli, A. Durmus, M. Pereyra and A. F. Vidal, “Efficient stochastic optimisation by unadjusted Langevin Monte Carlo. Application to maximum marginal likelihood and empirical Bayesian estimation”, Statistics and Computing, 31(3), 1-18, Mar. 2021.
• A. F. Vidal and M. Pereyra, “Maximum likelihood estimation of regularization parameters”, in 2018 IEEE International Conference on Image Processing (ICIP), pp. 1742-1746. IEEE, Oct. 2018.
• A. F. Vidal, L. Ciocci Brazzano, C. L. Matteo, P. A. Sorichetti and M. G. González, "Parametric modeling of wideband piezoelectric polymer sensors: Design for optoacoustic applications". Review of Scientific Instruments, 88(9), 095004, Sep. 2017.
• A. F. Vidal, M. G. González and P. Sorichetti, "Sensores piezoeléctricos para aplicaciones optoacústicas: Efectos de los procesos de relajación". In Proc. Biennial Congress of Argentina (ARGENCON), pp. 1-5. IEEE, Jun. 2016.